【コンピュータと２進数】




ふつう、私達が計算をするときには、０から９までの数字を使います。
どんなたくさんの数でも０から９までの数字の組み合わせで表せるからです。




ところが、コンピュータでは、このような１０進法だと仕組みが複雑になります。
そこで、今のコンピュータは、０と１だけで数を表す２進法を使います。




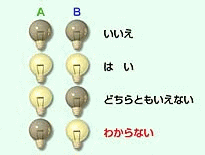たとえば、２つのランプを使って、質問への答えがハイであるときは、２つのランプを点灯する。
イイエのときは全部消す。答えられないときは、１つ点灯する。




このように、答えを表わし、点灯しているものを１、消えているランプを０とすると、０と１の組み合わせだけで４種類の答えが表わせます。
これが２進法です。







（1）　2進数と16進数

①　2進数

Oと1の2つの数字だけを用い、1の次は「10」となる数え方。
コンピューターの世界では、2進数によって演算が行われます。
電子回路のON／0FFや電圧の高低など、2つの状態を表すのに適しているためです。

1から順番にかぞえていくと、
02進数   0 １ 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 100001
10進数   0 １  2  3  4   5   6   7    8    9   10   11   12   13   14   15    16     となります。

2進数の「1110」は、10進数では 1×2^3 + 1×2^2 + 1×2^1 + 0　= 1×8 + 1×4 + 1×2 + 0×1= 14です。
また、2進数の1桁は「ビット」と呼ばれ、コンピューターで扱う数量の基本単位となります。


②　16進数

16で1桁繰り上がる数え方。
0～9までの10個の数字と、A～Fまでの6個の文字を用います。
文字コードなど、コンピューターで扱うデータの多くが16進数で表されます。
また、2進数の4桁分をまとめて16進数で表すこともあります。

1から順番にかぞえていくと、
16進数 0 １ 2 3 4 5 6 7 8 9  A  B  C  D   E  F  10
10進数 0 １ 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
となります。
16進数の「A1」は、10進数では 10×16 + 1で161です。
また、16進数の「1AD」は、10進数では、、
1AD = 1×16^2 + A×16^1 + D
= 1×256 + 10×16 + 13
= 429
になります。
16進数の使用例としては、インターネットの HTML ファイルがあります。
背景や文字の表示色を６桁の 16進数で指定しています。


③　10進数から２進数への変換

変換対象の10進数を２で割り、その商をさらに２で割っていきます。
これを商が２で割れなくなるまで繰り返し、最後の商を先頭にして、余りを並べていきます。
たとえば、100を２進数で表現するには、
１００÷２＝５０ 余り ０
５０÷２＝２５ 余り ０
２５÷２＝１２ 余り １
１２÷２＝６ 余り ０
６÷２＝３ 余り ０
３÷２＝１ 余り １
と最後の商が１で、もうこれ以上２で割ることはできません。
そこで、この商を先頭にして、各あまりを並べていきます。
すると100は２進数では、次のようになります。
１００＝１１００１００


④　10進数から16進数の変換

変換対象の10進数を16で割り、その商をさらに16で割っていきます。
これを商が16で割れなくなるまで繰り返し、最後の商を先頭にして、余りを並べていきます。
たとえば、100を16進数で表現するには、
１００÷１６＝６ 余り ４
これ以上商を16で割ることができません。
この商を先頭にしてあまりを並べると
１００＝６４
となります。
また、300を16進数で表現するには、、
３００÷１６＝１８ 余り １２
１８÷１６＝１ 余り ２
商をこれ以上16で割ることができません。
この商を先頭にしてあまりを並べていくと
３００＝１２Ｃ （Ｃ=12）
となります。
また、1963を16進数で表現するには、、
1963÷１６＝122 余り 11
122 ÷１６＝112 余り 10
112 ÷１６＝7 余り 0
商をこれ以上16で割ることができません。
この商を先頭にしてあまりを並べていくと
1963＝7AB（A=10、B=11）
となります。


⑤　２進数から16進数の変換

16進数は２進数の４桁をひとつにまとめたものと考えることができるので、２進数から16進数の変換は４桁ごとに変換します。
１１１１０００１０ であれば
０００１ １１１０ ００１０
最初の「０」３つは、４桁にそろえるため
というように４桁ごとに区切ります。この４桁ごと16進数に直していくと、
０００１＝１
１１１０＝Ｅ
(1×2^3 + 1×2^2 + 1×2^1 + 0　= 1×8 + 1×4 + 1×2 + 0×1= 14)
００１０＝２
(0×2^3 + 0×2^2 + 1×2^1 + 0　= 0×8 + 0×4 + 1×2 + 0×1= 2)
となるので、
０００１１１１０００１０＝１Ｅ２
となります。

⑥　16進数から２進数の変換
Ｅ２Ａ、
Ｅ＝１１１０
２＝００１０
Ａ＝１０１０
となるので、
Ｅ２Ａ＝１１１０００１０１０１０
と変換できます。



（2）　ビットとバイト

「0」と「1」を基本とした2進数の1桁をビット(bit)と呼びます。
コンピュータのメモリであれば、コンデンサ（蓄電器）に電荷が蓄積されている場合が「1」（1ビット）、
蓄積されていない場合が「0」（1ビット）となります。

コンピュータが1単位として扱うビットのまとまりのことをバイト(byte)と言います。
1バイトのビット数は、IBM社の規定に沿った1バイト＝8ビットが普及しています。

1ビットでは2通りの情報を表せますが、1バイトでは、2の8乗＝256通りの情報を表せます。
色に例えれば、1ビットでは白と黒の2色、2ビットでは4色、3ビットでは16色、8ビットでは256色の色を表現できるということです。

コンピュータでは、一般にファイル容量を表す単位として使用されています。
テキストファイルであれ、ワード文書であれ、 エクセルの文書であれ、GIF画像であれ、この「バイト」をもとにして構成されています。

1バイトは、元々はメモリ－CPU間の転送単位を意味していました。
たとえば、1B/s（bytes per second バイト毎秒）＝ 8bps （bits per second ビット毎秒）となります。

しかし、技術の進歩で転送単位が 8 → 16 → 32 → 64ビットと大きくなり、現在では転送単位とバイトは切り離して見る必要があります。

たとえば、32ビットのCPUは、2の32乗＝約43憶のデータ処理を一度に行えます。
処理速度でいえば、４GB/s （gigabytes per second ギガバイト毎秒）＝ 約43億B/s（バイト毎秒）となります。









Home Page